Word Puzzles with Neo4J
Stuck on a long train journey with only a single newspaper, my companion and I ran out of reading material and turned to the puzzle pages. One puzzle caught our attention: the “Word Morph”. Start with a four-letter word and turn it into another four letter word in a fixed number of steps, where at each step you can change only one letter in the word to create a new, valid word. For example, a puzzle may be to turn “HALT” into “SILO” in four steps. The solution is “HALT”, “SALT”, “SILT” and finally “SILO”.
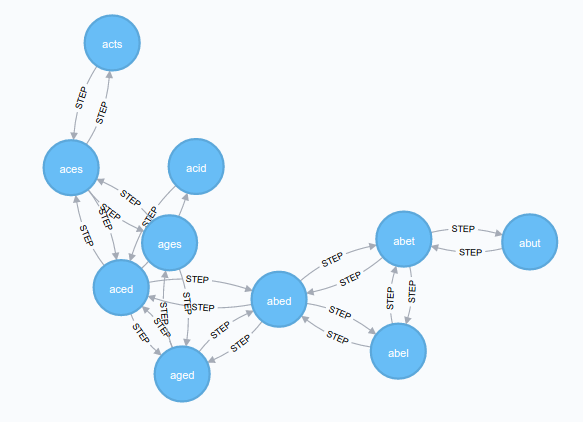
What interested me about this puzzle was that the domain can be be represented as a graph, with a node for every four-letter word and edges between every pair of words that differ by a single letter. Puzzles can then be solved by a path-finding algorithm.
So, I popped open my laptop and fired up Neo4J to experiment.
I first needed a list of all four-letter words. Linux stores dictionary files in /usr/share/dict/ and I could easily extract all the four-letter words with grep:
grep -E '^[[:alpha:]]{4}$' /usr/share/dict/british-english
The data was a bit dirty: it contained a mix of upper and lower case and some letters had accents. I cleaned it up with the unaccent command, normalised it to lowercase with tr, and ensured there were no duplicates with sort -u:
grep -E '^[[:alpha:]]{4}$' /usr/share/dict/british-english \
| unaccent utf-8 \
| tr [[:upper:]] [[:lower:]] \
| sort -u \
> puzzle-words
I then imported the data into Neo4J as CSV data (the list of words is a valid single-column CSV file). The Cypher command to load it into the database is:
load csv from "file:///<dir>/puzzle-words" as cols
create (:Word{word: cols[0]})
That gave me about 3000 nodes in my database, one for each word, but they were not yet linked by any relationships.
I needed to link the words that are different by a single letter. The database is tiny, so brute-forcing the calculation for all pairs of words was practical in the time available, despite being O(n2) in the number of words.
The trickiest bit was calculating the number of letter differences between two words. Unsurprisingly, Cypher doesn’t have a built-in function for this. Unlike SQL, Cypher does have some nice functional programming constructs that can be used to perform calculations: list comprehensions, EXTRACT (Cypher’s term for map), REDUCE (fold), COLLECT (used to turn rows of a result set into a collection) and UNWIND (used to turn a collection into rows in the result set). I used a list comprehension to create a list of indices where the letters of two words differ. The number of differences was then the length of this list.
Given all pairs of words and the number of letter differences between the words in each pair, I created edges between the words (both ways) if there was a single letter difference:
match (w1:Word), (w2:Word)
where w2.word > w1.word
with w1, w2,
length([i in range(0,3) where substring(w1.word,i,1) <> substring(w2.word,i,1)]) as diffCount
where diffCount = 1
create (w1)-[:STEP]->(w2)
create (w2)-[:STEP]->(w1)
That completed the data model. Now solving a puzzle was a simple Cypher query using the shortestPath function:
match
(start {word:'halt'}),
(end {word:'silo'}),
p = shortestPath((start)-[*..3]->(end))
unwind nodes(p) as w
return w.word as step
Giving:
step
----
halt
salt
silt
silo
Returned 4 rows in 121 ms.
Success!
But my travelling companion was not happy. She didn’t want a computer program to solve the puzzle. She wanted to solve it herself. I’d ruined that. It looked like the rest of the train journey was going to pass amid a somewhat frosty atmosphere!
But the same graph model that solves puzzles can be used to generate new puzzles:
match (w)
with collect(w) as words
with words[toInt(rand()*length(words))] as start
match p = start -[*3]-> (end)
with collect(p) as puzzles
with extract(n in nodes(puzzles[toInt(rand()*length(puzzles))]) | n.word) as puzzle
unwind puzzle as step
return step
Again, a brute-force approach to selecting random words and puzzles that only works because of the tiny dataset1. And the query picks a random starting word without looking at its relationships with other words, so sometimes picks a word that cannot be morphed into another by three steps and returns an empty resultset. So, not perfect but good enough to pass the time until the end of the journey.
For a more serious application of Neo4J, James Richardson and I gave a talk at ACCU2014 on how we used Neo4J to analyse the heap memory use of embedded Java code in Sky’s PVR system.
Update: I found another implementation of this puzzle, which uses Java to build the graph and the Neo4J Java traversal API to solve puzzles. I’m struck how far Neo4J and Cypher have come since 2014, when that article was written. Cypher’s CSV import and functional programming constructs make it possible to solve the puzzle without any Java programming at all. Neo4J has become one of my go-to tools for quick-but-not-dirty data analysis.
It would be great if a future version Neo4J added an operator for returning random rows of the result set↩︎
