Faster Word Puzzles with Neo4J

When I used Neo4J to create and solve Word Morph puzzles, I brute-forced the algorithm to find and link words that differ by one letter. I was lucky – my dataset only contained four-letter words and so was small enough for my O(n²) algorithm to run in a reasonable amount of time. But what happens when I expand my dataset to include words of 4, 5 and 6 letters?

Obviously, I have to change my Cypher to only relate words that are the same length:

          match (w1), (w2) 
where w2.word > w1.word 
  and length(w1.word) = length(w2.word)
with 
  w1, 
  w2, 
  length([i in range(0,length(w1.word)) 
          where substring(w1.word,i,1) <> substring(w2.word,i,1)]) 
    as diffCount
where diffCount = 1
create (w1)-[:STEP]->(w2)
create (w2)-[:STEP]->(w1)
        

But with the larger dataset, this query takes a very long time to run. I don’t know how long – I’ve never been patient enough to wait for the query to complete. I need a better algorithm.

Nikhil Kuriakose has also written about solving these puzzles with Neo4J. He used a more sophisticated algorithm to create the graph. He first grouped words into equivalence classes, each of which contains words that are the same except at one letter position. So, for instance, the class P_PE would contain PIPE, POPE, etc., the class PIP_ would contain PIPE, PIPS, etc., and so on. He then created relationships between all the words in each equivalence class.

This also has a straightforward representation as a property graph. An Equivalence class can be represented by an Equivalence node with a pattern property, and a word’s membership of an equivalence class can be represented by a relationship from the Word node to the Equivalence node.

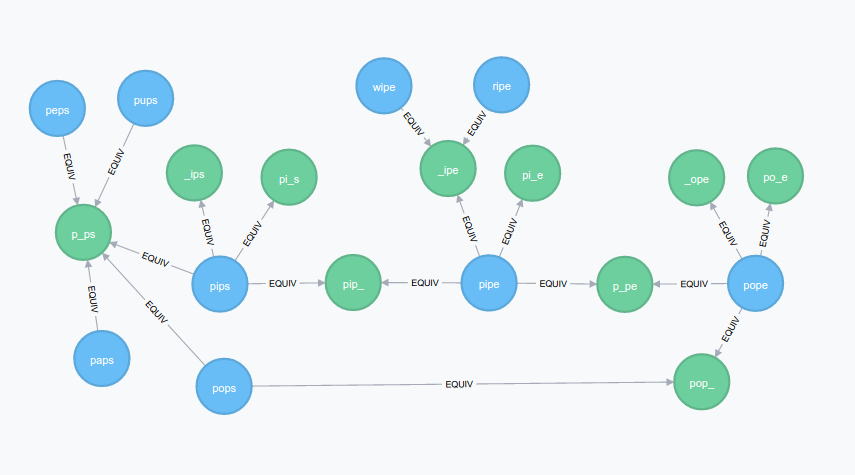
Nikhil implemented the algorithm in Java, grouping words with a HashMap and ArrayLists before loading them into Neo4J. But by modelling equivalence classes in the graph, I can implement the algorithm in Cypher – no Java required. For each Word in the database, my Cypher query calculates the patterns of the equivalence classes that the word belongs to, creates Equivalence nodes if for the patterns, and creates an :EQUIV relationship from the Word node to each Equivalence node. The trick is to only create Equivalence nodes for a pattern once, when one doesn’t yet exist, and subsequently use the same Equivalence node for the same pattern. This is achieved by creating Equivalence nodes with Cypher’s MERGE clause.

MERGE either matches existing nodes and binds them, or it creates new data and binds that. It’s like a combination of MATCH and CREATE that additionally allows you to specify what happens if the data was matched or created.

Before using MERGE, I must define a uniqueness constraint on the pattern property of the Equivalence nodes that will be used to identify nodes in the MERGE command. This makes Neo4J create an index for the property and ensures that the merge has reasonable performance.

          create constraint on (e:Equivalence) assert e.pattern is unique
        

Then I relate all the Word nodes in my database to Equivalence nodes:

          match(w:Word)
unwind [i in range(0,length(w.word)-1) | 
          substring(w.word,0,i)+"_"+substring(w.word,i+1)] 
  as pattern
merge (e:Equivalence {pattern:pattern})
create (w)-[:EQUIV]->(e)
        

This takes about 15 seconds to run. Much less time for my large dataset than my first, brute-force approach took for the small dataset of only four-letter words.

Now that the words are related to their equivalence classes, there is no need to create relationships between the words directly. I can query via the Equivalence nodes:

          match (start {word:'halt'}), (end {word:'silo'}),
  p = shortestPath((start)-[*]-(end))
  unwind [n in nodes(p)|n.word] as step
  with step where step is not null
  return step
        

Giving:

          step
----
halt
hilt
silt
silo

Returned 4 rows in 897 ms.
        

And it now works for longer words:

          step
----
candy
bandy
bands
bends
beads
bears
hears
heart

Returned 8 rows in 567 ms.
        

load csv from "file:///<dir>/puzzle-words.csv" as l
create (w:Word{word:l[0]})
with w
unwind [i in range(0,length(w.word)-1) | 
          substring(w.word,0,i)+"_"+substring(w.word,i+1)] 
  as pattern
merge (e:Equivalence {pattern:pattern})
create (w)-[:EQUIV]->(e)

Copyright © 2015 Nat Pryce. Posted 2015-04-19. Share it.